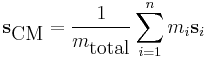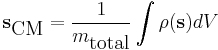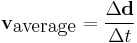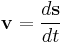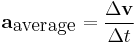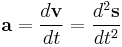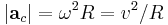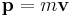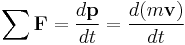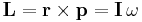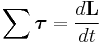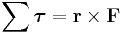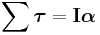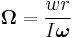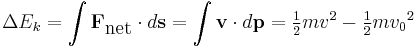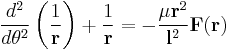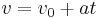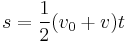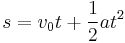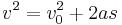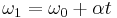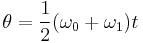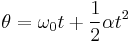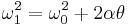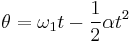List of equations in classical mechanics
- Nomenclature
- a = acceleration (m/s²)
- g = gravitational field strength/acceleration in free-fall (m/s²)
- F = force (N = kg m/s²)
- Ek = kinetic energy (J = kg m²/s²)
- Ep = potential energy (J = kg m²/s²)
- m = mass (kg)
- p = momentum (kg m/s)
- s = displacement (m)
- R = radius (m)
- t = time (s)
- v = velocity (m/s)
- v0 = velocity at time t=0
- W = work (J = kg m²/s²)
- τ = torque (m N, not J) (torque is the rotational form of force)
- s(t) = position at time t
- s0 = position at time t=0
- runit = unit vector pointing from the origin in polar coordinates
- θunit = unit vector pointing in the direction of increasing values of theta in polar coordinates
Note: All quantities in bold represent vectors.
Classical mechanics is the branch of physics used to describe the motion of macroscopic objects.[1] It is the most familiar of the theories of physics. The concepts it covers, such as mass, acceleration, and force, are commonly used and known.[2] The subject is based upon a three-dimensional Euclidean space with fixed axes, called a frame of reference. The point of concurrency of the three axes is known as the origin of the particular space.[3]
Classical mechanics utilises many equations—as well as other mathematical concepts—which relate various physical quantities to one another. These include differential equations, manifolds, Lie groups, and ergodic theory.[4] This page gives a summary of the most important of these.
Contents[hide] |
Equations
Name of equation |
Equation | Year derived[5] |
Derived by |
Notes |
|---|---|---|---|---|
| Center of mass | Discrete case:
where n is the number of mass particles. Continuous case: where ρ(s) is the scalar mass density as a function of the position vector |
1687 | Isaac Newton |
Velocity
average velocity = change in distance / change in time.
Acceleration
- Centripetal Acceleration
(R = radius of the circle, ω = v/R angular velocity)
Momentum
Force
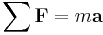 (Constant Mass)
(Constant Mass)
Impulse
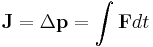
-
if F is constant
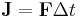
Moment of inertia
For a single axis of rotation: The moment of inertia for an object is the sum of the products of the mass element and the square of their distances from the axis of rotation:
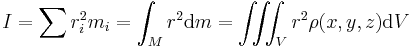
Angular momentum
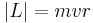 if v is perpendicular to r
if v is perpendicular to r
Vector form:
(Note: I can be treated like a vector if it is diagonalized first, but it is actually a 3×3 matrix - a tensor of rank-2)
r is the radius vector.
Torque
if |r| and the sine of the angle between r and p remains constant.
This one is very limited, more added later. α = dω/dt
Precession
Omega is called the precession angular speed, and is defined:
(Note: w is the weight of the spinning flywheel)
Energy
for m as a constant:
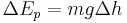 in field of gravity
in field of gravity
Central force motion
Equations of motion (constant acceleration)
These equations can be used only when acceleration is constant. If acceleration is not constant then calculus must be used.
These equations can be adapted for angular motion, where angular acceleration is constant:
See also
Notes
- ^ Mayer, Sussman & Wisdom 2001, p. xiii
- ^ Berkshire & Kibble 2004, p. 1
- ^ Berkshire & Kibble 2004, p. 2
- ^ Arnold 1989, p. v
- ^ Note that this is the year the person(s) who derived it published their work, not the year that they originally discovered it.
References
- Arnold, Vladimir I. (1989), Mathematical Methods of Classical Mechanics (2nd ed.), Springer, ISBN 978-0-387-96890-2
- Berkshire, Frank H.; Kibble, T. W. B. (2004), Classical Mechanics (5th ed.), Imperial College Press, ISBN 978-1860944352
- Mayer, Meinhard E.; Sussman, Gerard J.; Wisdom, Jack (2001), Structure and Interpretation of Classical Mechanics, MIT Press, ISBN 978-0262194556